Equivalence testing

Inception

  • Commonly used in pharmaceutical development (Berger and Hsu 1996)

Classical hypothesis testing

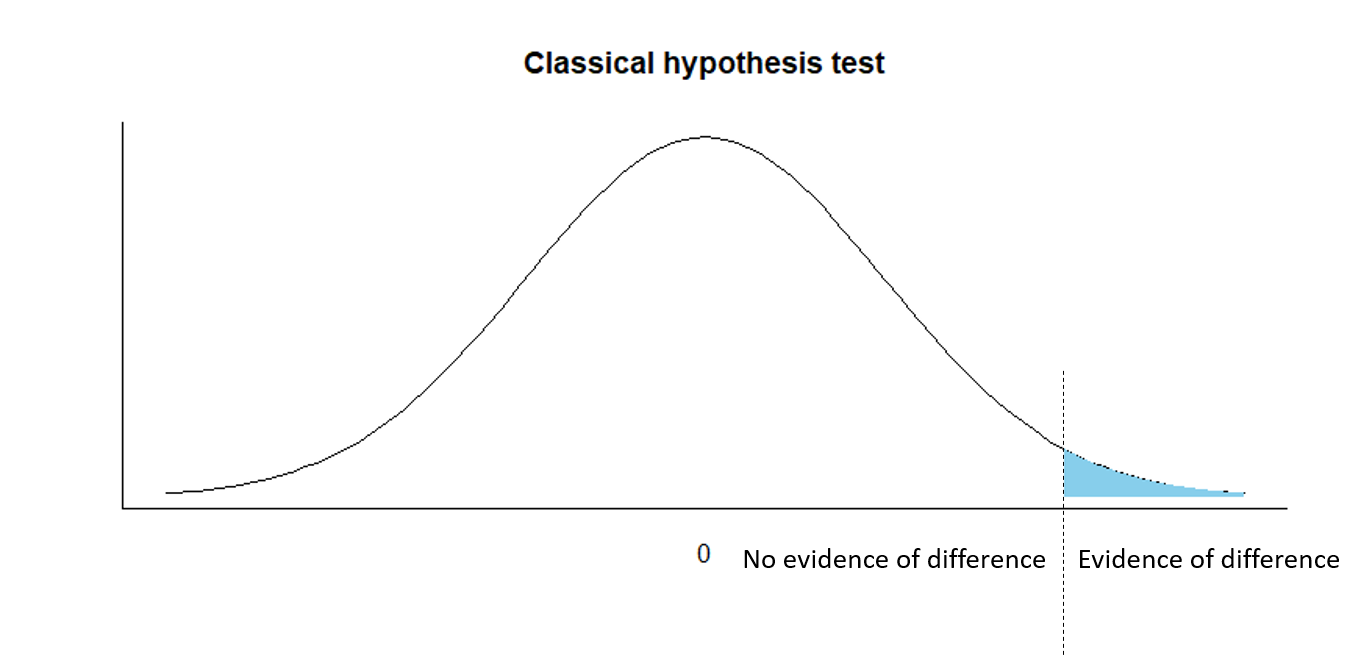
$H_0: d = 0$ <br> $H_a: d > 0$

\(H_0: d = 0\)
\(H_a: d > 0\)

Classical hypothesis testing

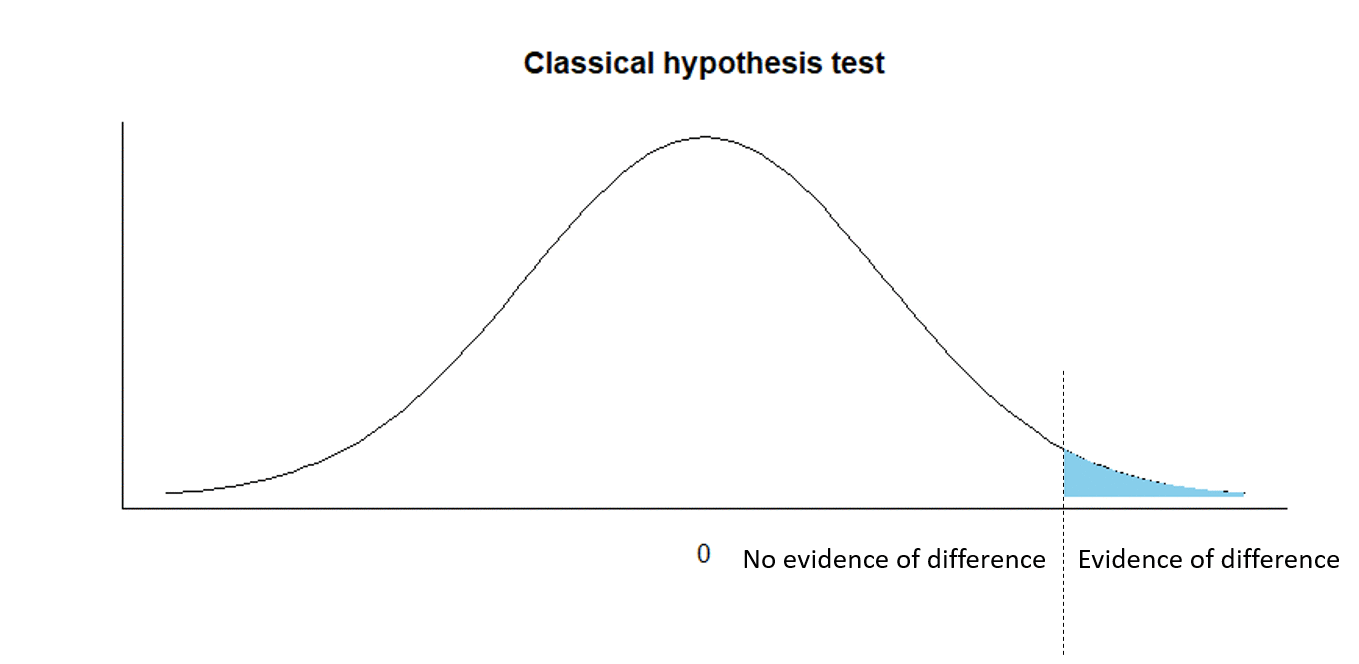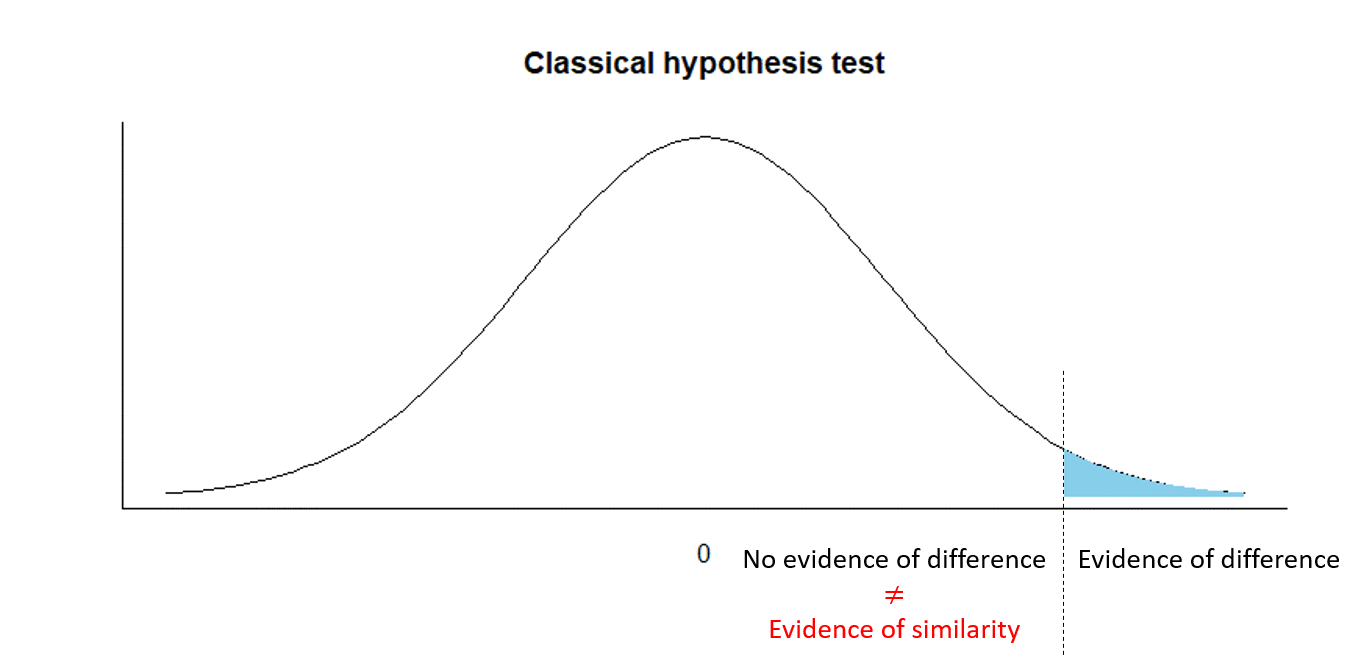
$H_0: d = 0$ <br> $H_a: d > 0$

\(H_0: d = 0\)
\(H_a: d > 0\)

Equivalence testing

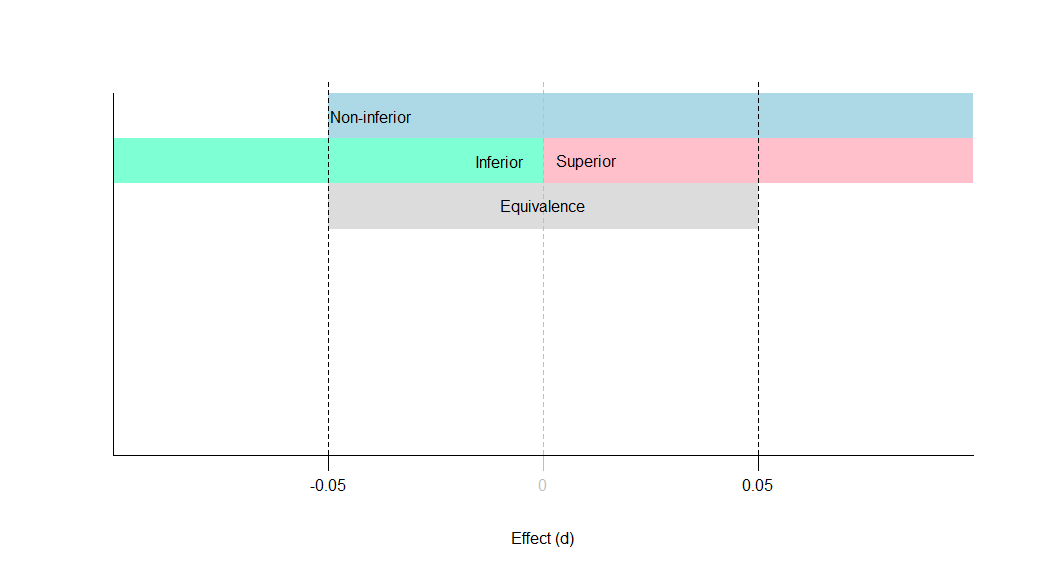
$H_0: d \le -0.05 \text{ or } d \ge 0.05$ <br> $H_a: -0.05 < d < 0.05$

\(H_0: d \le -0.05 \text{ or } d \ge 0.05\)
\(H_a: -0.05 < d < 0.05\)

Equivalence testing

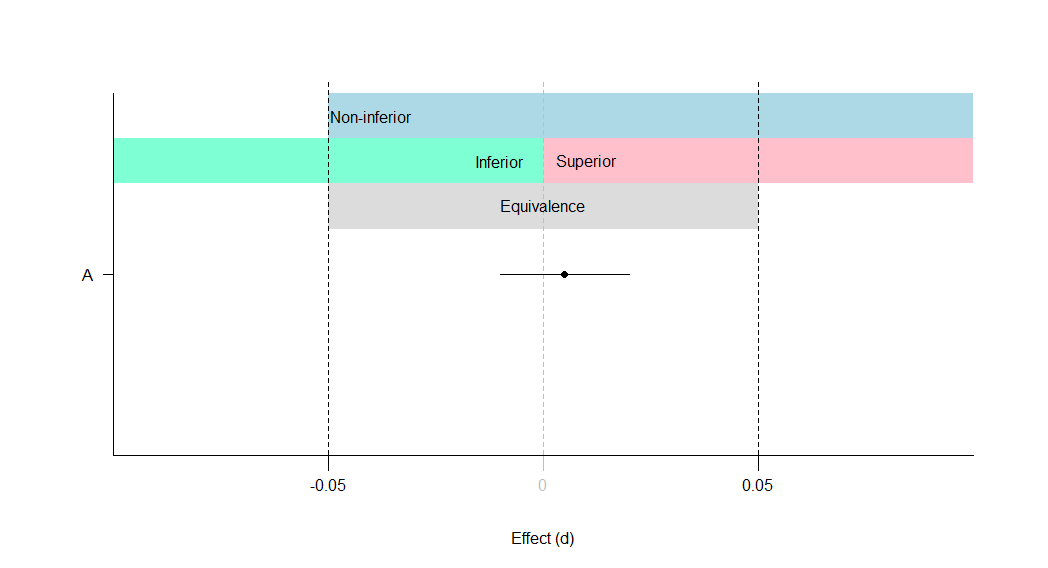
A: Equivalent and not significant (effect is **equivalent**)

A: Equivalent and not significant (effect is equivalent)

Equivalence testing

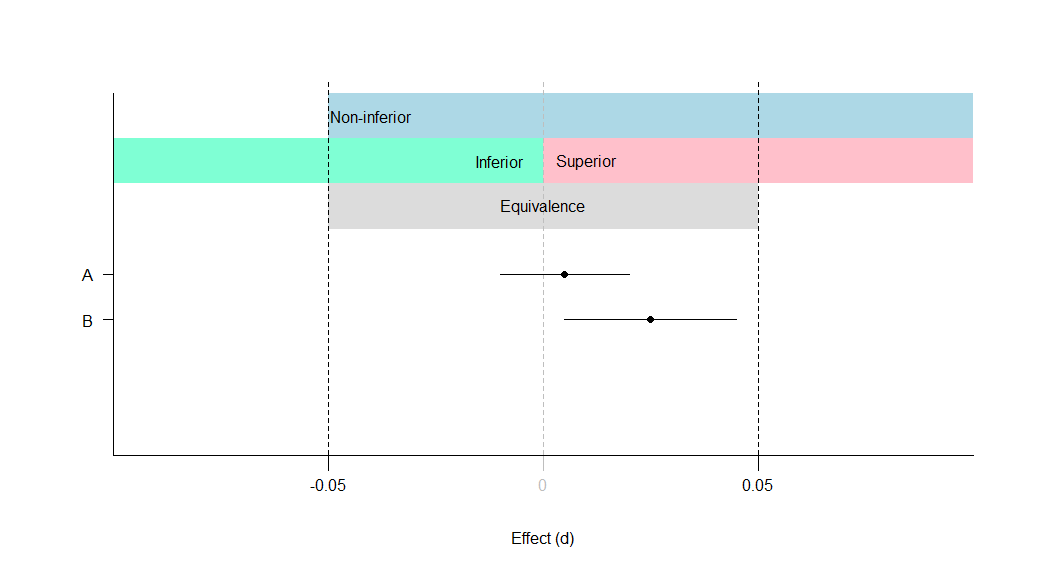
A: Equivalent and not significant (effect is **equivalent**) <br> B: Equivalent and significant (effect is **equivalent**)

A: Equivalent and not significant (effect is equivalent)
B: Equivalent and significant (effect is equivalent)

Equivalence testing

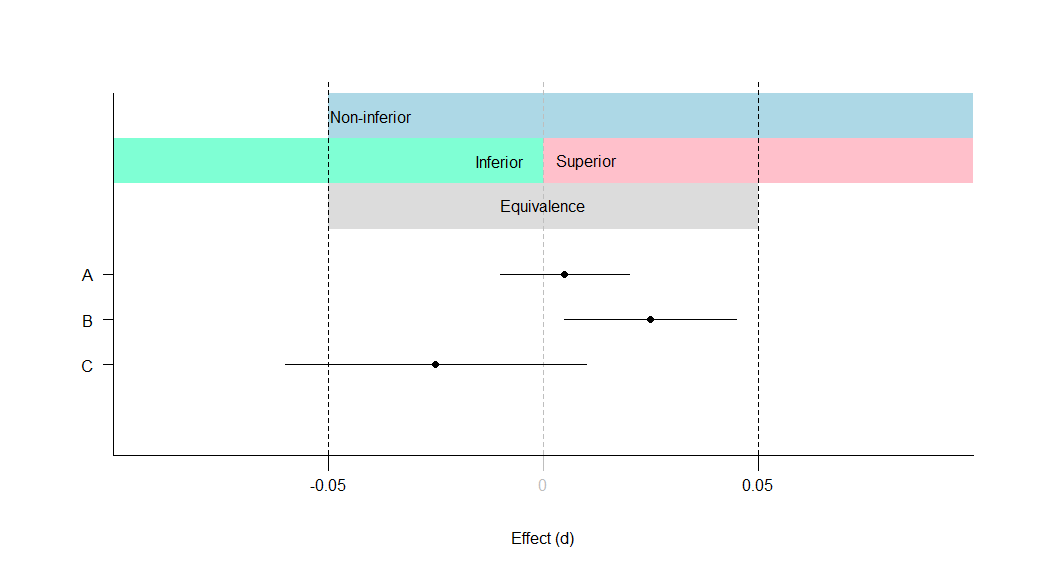
A: Equivalent and not significant (effect is **equivalent**) <br> B: Equivalent and significant (effect is **equivalent**) <br> C: Not equivalent and not significant (effect is **inconclusive**)

A: Equivalent and not significant (effect is equivalent)
B: Equivalent and significant (effect is equivalent)
C: Not equivalent and not significant (effect is inconclusive)

Equivalence testing

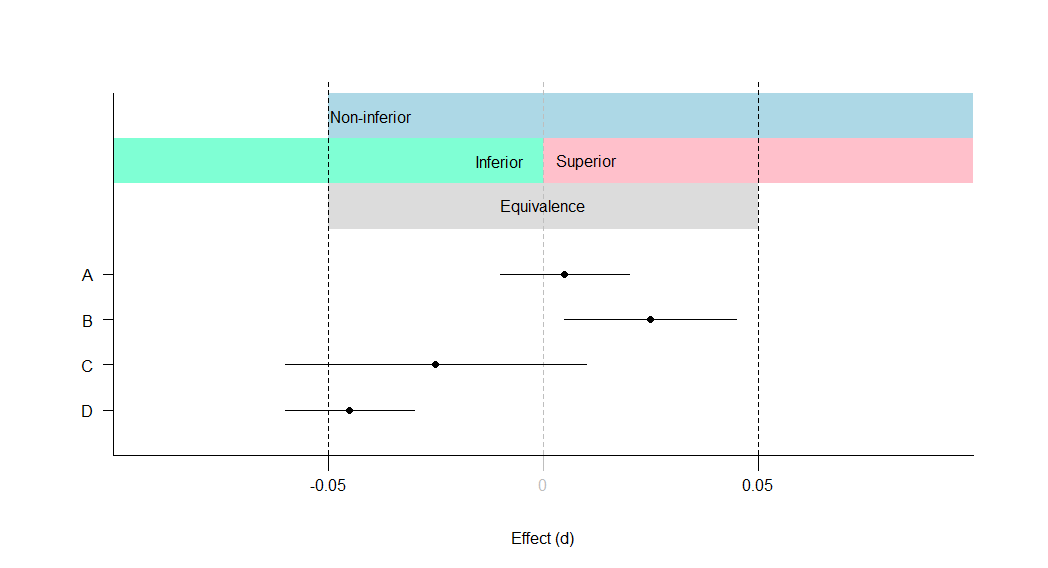
A: Equivalent and not significant (effect is **equivalent**) <br> B: Equivalent and significant (effect is **equivalent**) <br> C: Not equivalent and not significant (effect is **inconclusive**) <br> D: Not equivalent and significant (effect is **inferior**)

A: Equivalent and not significant (effect is equivalent)
B: Equivalent and significant (effect is equivalent)
C: Not equivalent and not significant (effect is inconclusive)
D: Not equivalent and significant (effect is inferior)

Equivalence testing

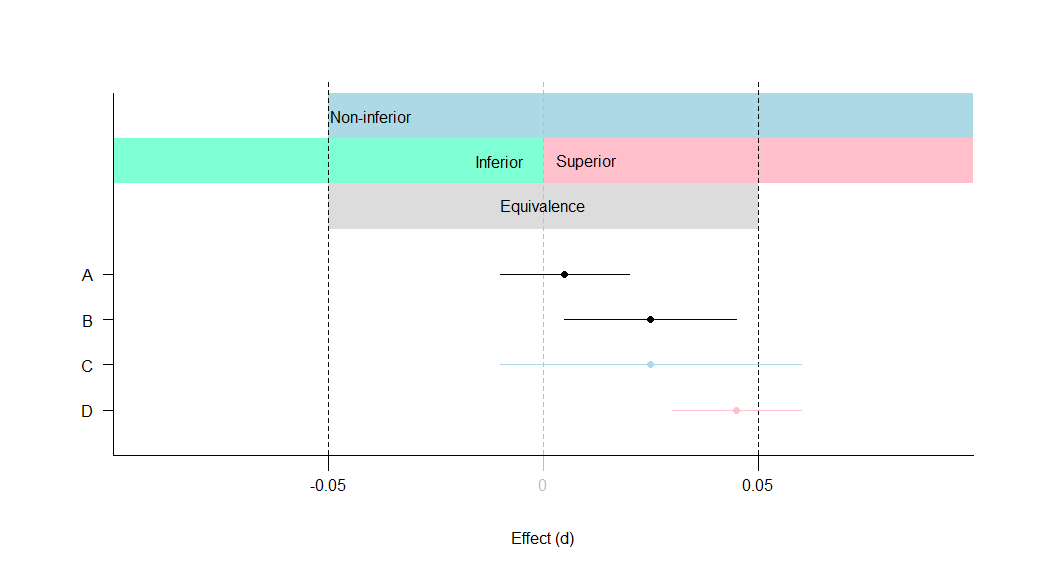
A: Equivalent and not significant (effect is **equivalent**) <br> B: Equivalent and significant (effect is **equivalent**) <br> C: Not equivalent and not significant (effect is **non-inferior**) <br> D: Not equivalent and significant (effect is **superior**)

A: Equivalent and not significant (effect is equivalent)
B: Equivalent and significant (effect is equivalent)
C: Not equivalent and not significant (effect is non-inferior)
D: Not equivalent and significant (effect is superior)

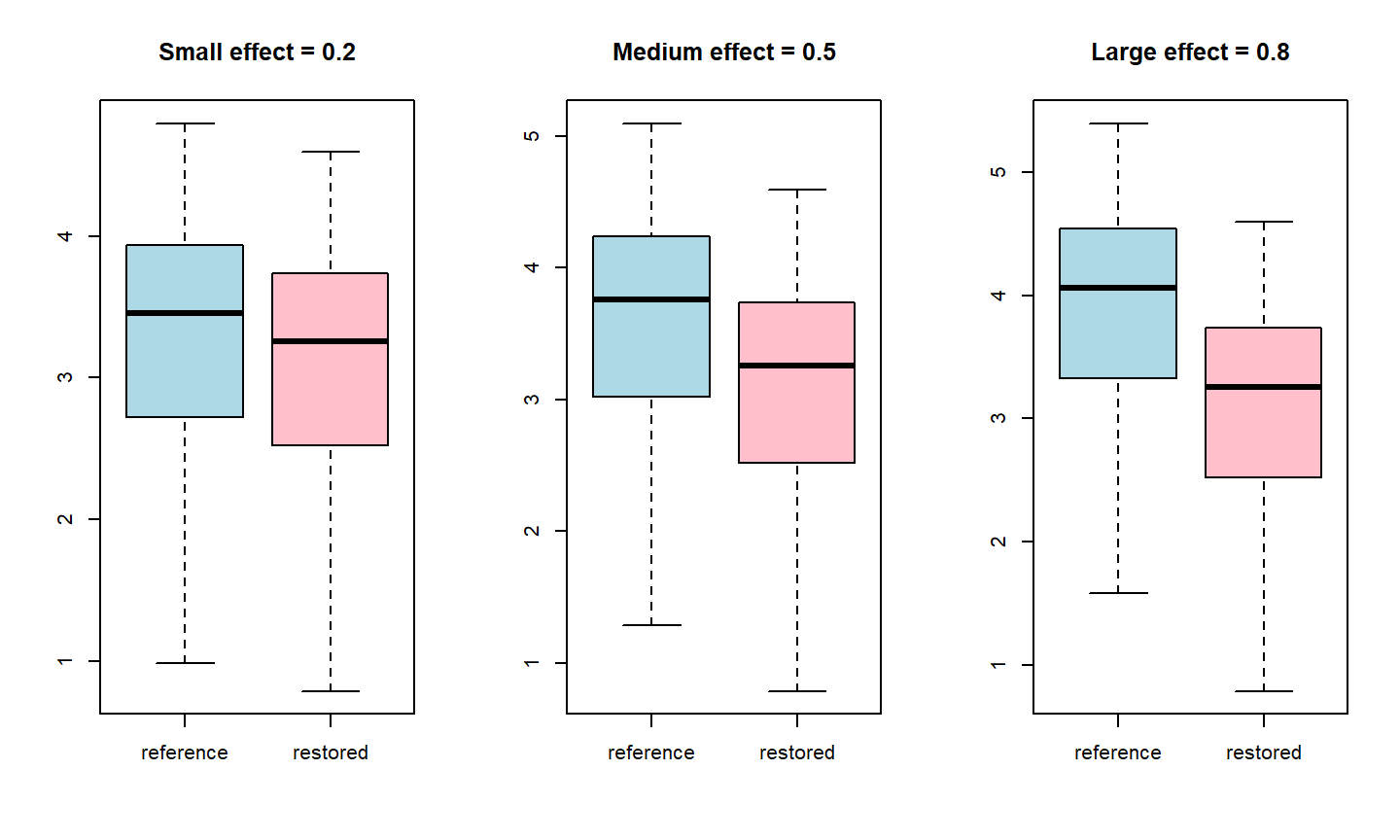
How to set the bounds?

  • What is your effect size of interest?
  • Cohen’s small-medium-large effect thresholds
    • Small effect = 0.2
    • Medium effect = 0.5
    • Large effect = 0.8

  • Always pre-specify!

Ecological restoration

  • Restoration can be considered successful if there is evidence of similarity between the restored and reference sites

Operation Crayweed

The problem

Operation Crayweed

The solution

Reference site

Reference site

Restored site

Restored site

Locations

Locations

TOSTER

Install packages

install.packages(c('TOSTER', 'ecoCopula', 'mvabund', 'devtools'))
devtools::install_github('lsjmichelle/ecopower@1e5d39a')

Load package

library(TOSTER)

Species richness data

data('crayweed', package='ecopower')
abund = crayweed$abund
X = crayweed$X

data = data.frame(richness = rowSums(abund>0))
data$treatment = X$treatment
data$treatment = factor(data$treatment, levels=c('restored', 'reference'))
head(data)
##   richness treatment
## 1        8 reference
## 2        5  restored
## 3        9  restored
## 4       15 reference
## 5        9 reference
## 6       12  restored

TOSTER

Specifying the effect - Cohen’s d

TOSTER

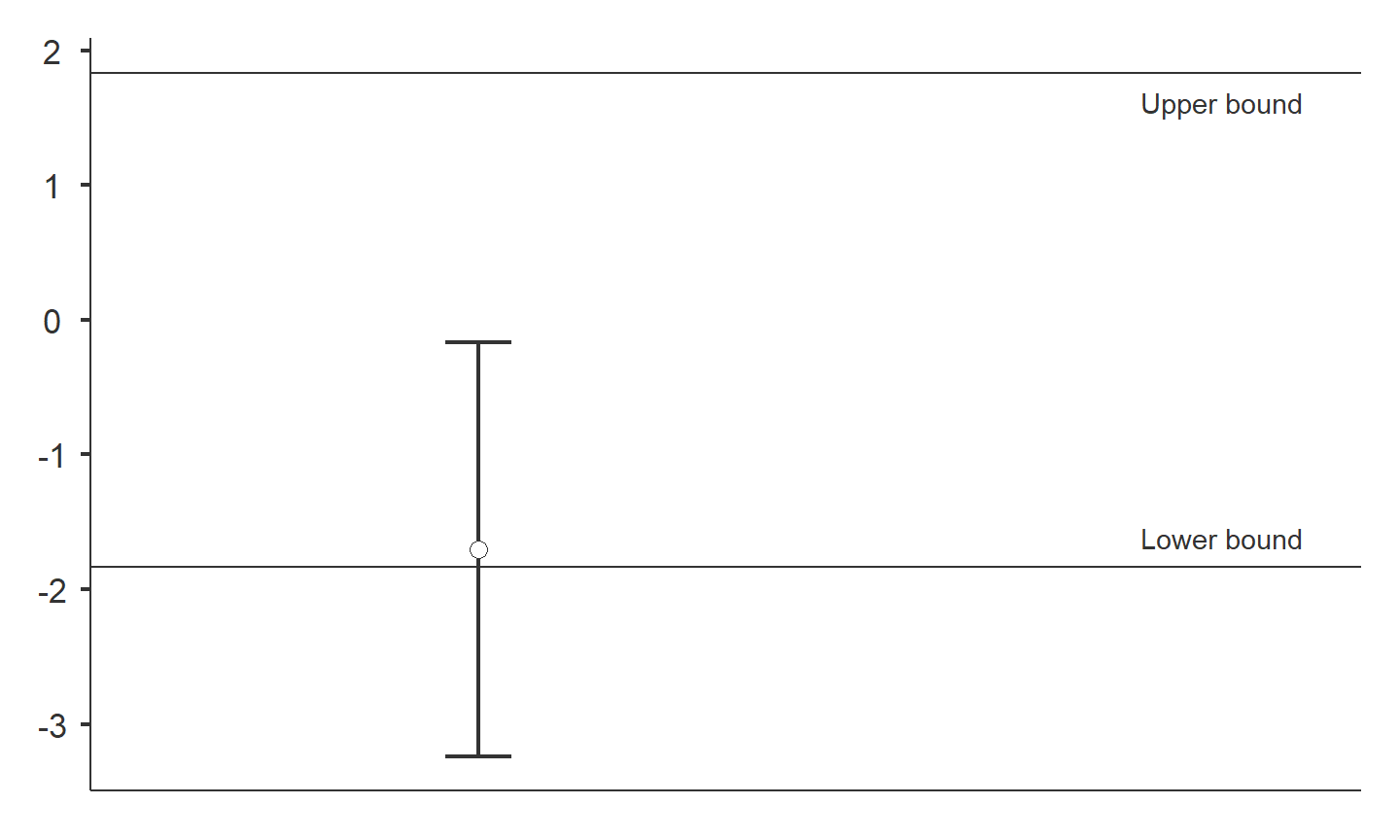
Testing for equivalence

dataTOSTtwo(
  data, deps='richness', group='treatment',
  low_eqbound=-0.8, high_eqbound=0.8,
  var_equal=TRUE, desc=TRUE, plots=TRUE
)
## 
##  TOST INDEPENDENT SAMPLES T-TEST
## 
##  TOST Results                                                     
##  ---------------------------------------------------------------- 
##                              t            df          p           
##  ---------------------------------------------------------------- 
##    richness    t-test        -1.895899    25.00000    0.0695896   
##                TOST Upper    -3.938410    25.00000    0.0002901   
##                TOST Lower    0.1466122    25.00000    0.4423070   
##  ---------------------------------------------------------------- 
## 
## 
##  Equivalence Bounds                                                              
##  ------------------------------------------------------------------------------- 
##                             Low           High         Lower        Upper        
##  ------------------------------------------------------------------------------- 
##    richness    Cohen's d    -0.8000000    0.8000000                              
##                Raw           -1.836360     1.836360    -3.240283    -0.1688077   
##  ------------------------------------------------------------------------------- 
## 
## 
##  Descriptives                                                         
##  -------------------------------------------------------------------- 
##                 N     Mean        Median      SD          SE          
##  -------------------------------------------------------------------- 
##    restored     11    9.545455    11.00000    2.339386    0.7053514   
##    reference    16    11.25000    12.00000    2.265686    0.5664215   
##  --------------------------------------------------------------------

TOSTER

Too few samples?

powerTOSTtwo(alpha=0.05, N=14, low_eqbound_d=-0.8, high_eqbound_d=0.8)
## The statistical power is 36.31 % for equivalence bounds of -0.8 and 0.8 .
## [1] 0.3630618
powerTOSTtwo(alpha=0.05, statistical_power=0.8, low_eqbound_d=-0.8, high_eqbound_d=0.8)
## The required sample size to achieve 80 % power with equivalence bounds of -0.8 and 0.8 is 27 per group, or 54 in total.
## [1] 26.76202

TOSTER

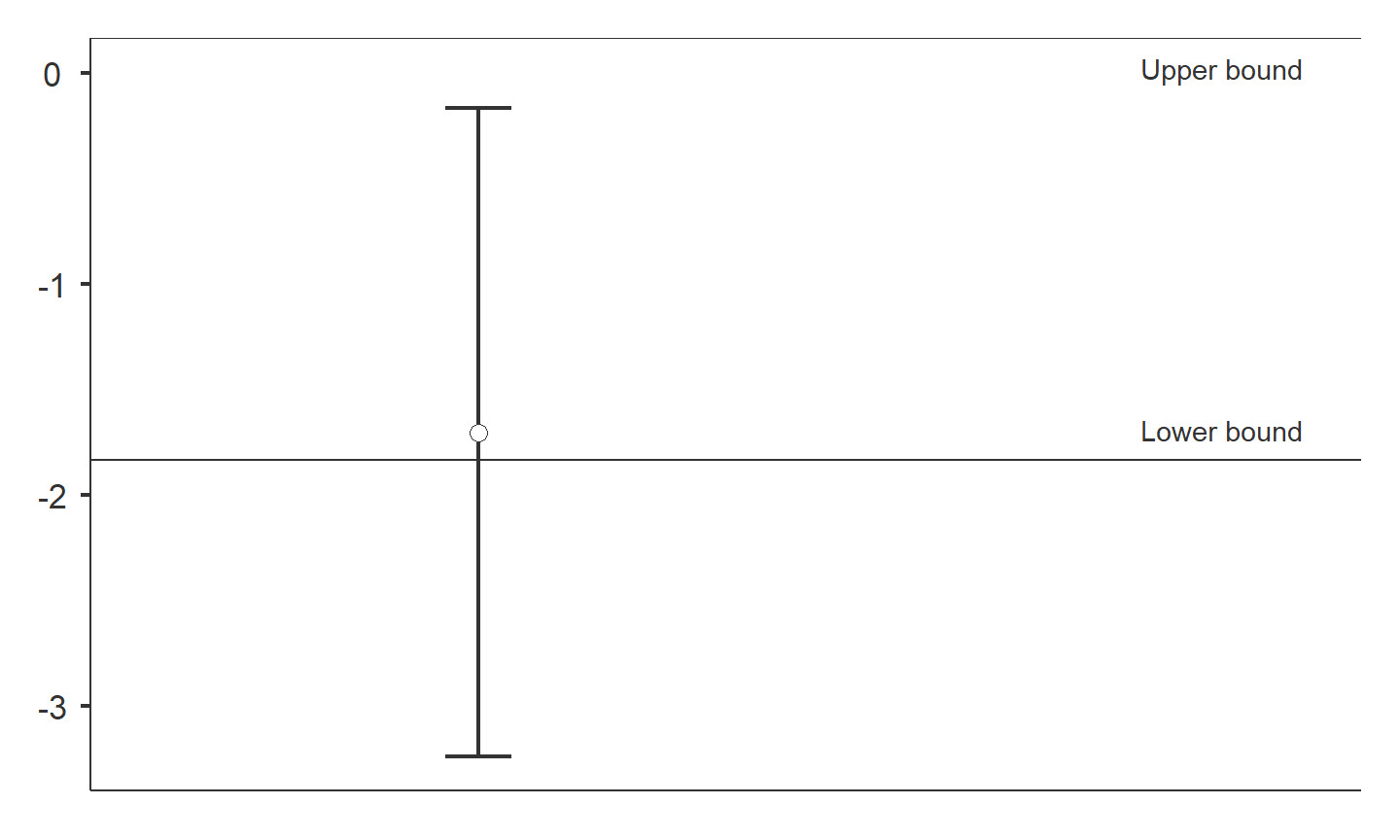
Testing for non-inferiority

dataTOSTtwo(
  data, deps='richness', group='treatment',
  low_eqbound=-0.8, high_eqbound=Inf,
  var_equal=TRUE, desc=TRUE, plots=TRUE
)
## 
##  TOST INDEPENDENT SAMPLES T-TEST
## 
##  TOST Results                                                      
##  ----------------------------------------------------------------- 
##                              t            df          p            
##  ----------------------------------------------------------------- 
##    richness    t-test        -1.895899    25.00000     0.0695896   
##                TOST Upper         -Inf    25.00000    < .0000001   
##                TOST Lower    0.1466122    25.00000     0.4423070   
##  ----------------------------------------------------------------- 
## 
## 
##  Equivalence Bounds                                                         
##  -------------------------------------------------------------------------- 
##                             Low           High    Lower        Upper        
##  -------------------------------------------------------------------------- 
##    richness    Cohen's d    -0.8000000     Inf                              
##                Raw           -1.836360     Inf    -3.240283    -0.1688077   
##  -------------------------------------------------------------------------- 
## 
## 
##  Descriptives                                                         
##  -------------------------------------------------------------------- 
##                 N     Mean        Median      SD          SE          
##  -------------------------------------------------------------------- 
##    restored     11    9.545455    11.00000    2.339386    0.7053514   
##    reference    16    11.25000    12.00000    2.265686    0.5664215   
##  --------------------------------------------------------------------

Multivariate equivalence testing

cbind(abund[1:6,2:4], head(X))
##   Acanthopagrus.australis Acanthurus.nigrofuscus Achoerodus.viridis treatment time
## 1                       0                      0                  1 reference    1
## 2                       0                      0                  0  restored    1
## 3                       0                      0                  0  restored    1
## 4                       0                      0                  0 reference    1
## 5                       0                      0                  1 reference    2
## 6                       3                      0                  1  restored    2
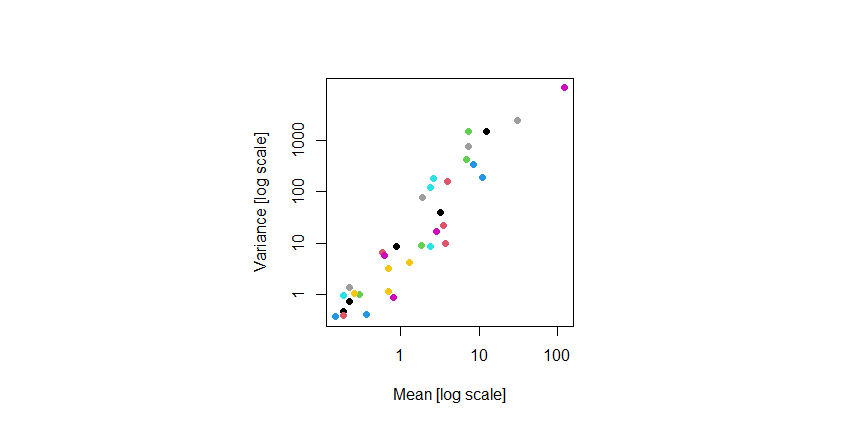
Mean-variance relationship

Mean-variance relationship

Multivariate equivalence testing

How to specify the effect?

Problem: Each species has its own parameter to estimate effect size. How do we decide what effect size to use for each species?

Multivariate equivalence testing

Specifying the effect

  • Solution: Classify each species as an
    • increaser
    • decreaser
    • no-effect
  • Assume a constant effect size (e.g. 50% change in mean abundance)

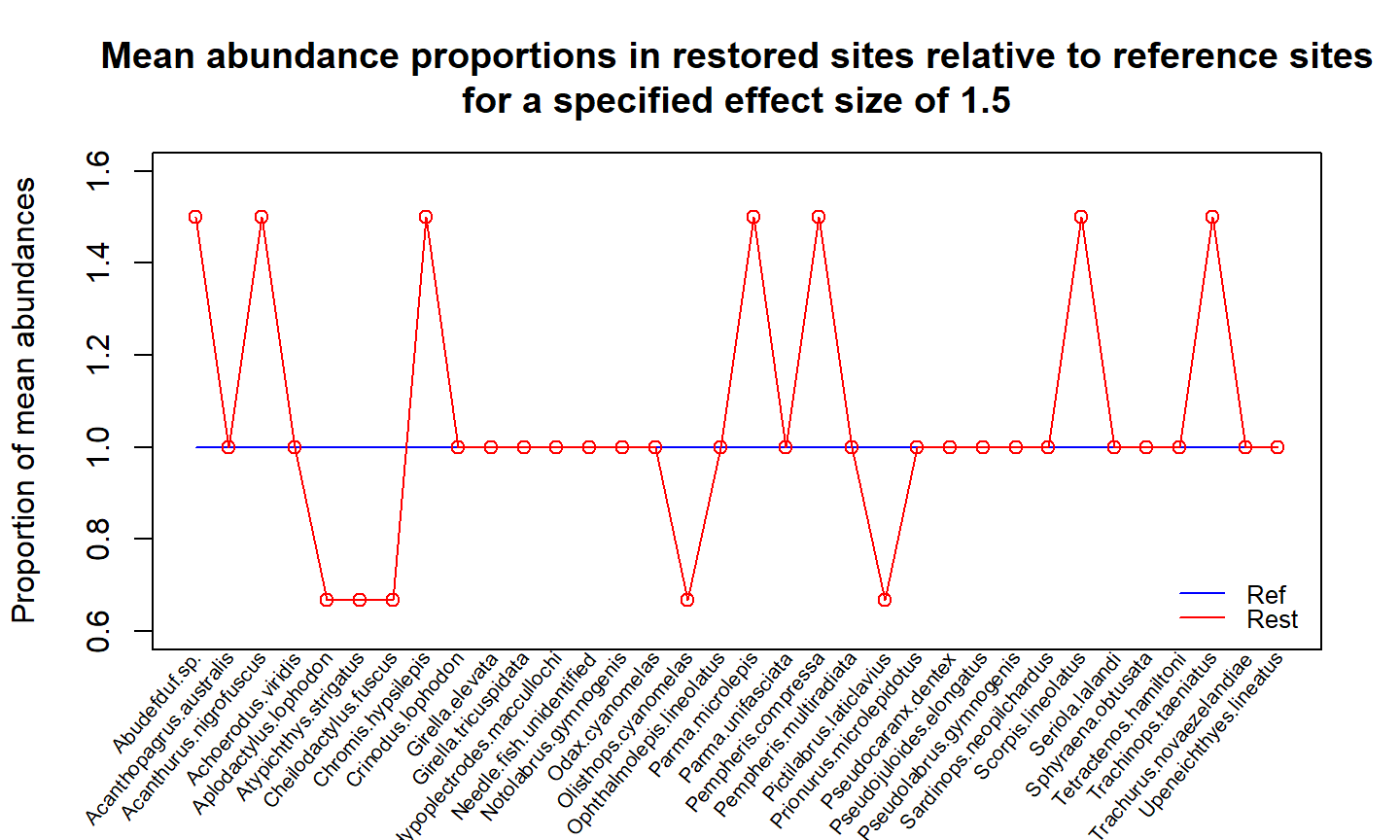
Multivariate equivalence testing

We will use the ecopower package, which fits a copula model (Popovic, Hui, and Warton 2018).

library(ecopower)
library(ecoCopula)
library(mvabund)
Copula models have two steps:

  1. Fit a marginal model (separate for each species)

    fit = manyglm(abund ~ time + treatment, family='negative.binomial', data=X)

  2. Fit a correlation model (to residuals)

    fit.cord = cord(fit)

Multivariate equivalence testing

Specifying the effect

increasers = c(
  'Abudefduf.sp.', 'Acanthurus.nigrofuscus', 'Chromis.hypsilepis',
  'Parma.microlepis', 'Pempheris.compressa', 'Scorpis.lineolatus',
  'Trachinops.taeniatus'
)

decreasers = c(
  'Aplodactylus.lophodon', 'Atypichthys.strigatus', 'Cheilodactylus.fuscus',
  'Olisthops.cyanomelas', 'Pictilabrus.laticlavius'
)

effect_mat = effect_alt(fit, effect_size=1.5, increasers, decreasers, term='treatment')

Multivariate equivalence testing

equivtest(fit.cord, coeffs=effect_mat)
## Time elapsed: 0 hr 0 min 44 sec
## Equivalence Test Table
## 
## object0: abund ~ time
## object: abund ~ time + treatment
## 
## Multivariate test:
##         Res.Df Df.diff   Dev Pr(>Dev)
## object0     20                       
## object      19       1 128.9        1
## Arguments:
##  Test statistics calculated assuming uncorrelated response (for faster computation) 
## P-value calculated using 999 Monte Carlo samples from a factor analytic Gaussian copula 
## Effect sizes taken from user-entered coefficient matrix, for details apply coef function to this object

Conclusion

  • Equivalence test is useful when we want evidence of similiarity
  • The key step is specifying effect size. Harder for multivariate data!
  • Try TOSTER for univariate equivalence tests
  • Try equivtest in ecopower on GitHub for multivariate abundances
devtools::install_github('lsjmichelle/ecopower@1e5d39a')

Thank you!

References

Berger, R. L., and J. C. Hsu. 1996. “Bioequivalence Trials, Intersection-Union Tests and Equivalence Confidence Sets.” Statistical Science 11 (4): 283–302.

Popovic, G. C., F. K. C Hui, and D. I. Warton. 2018. “A General Algorithm for Covariance Modeling of Discrete Data.” Journal of Multivariate Analysis 165: 86–100.